Group Leader: Jacques Vigué
Matthias Büchner, Marion Jacquey, Gérard Trénec
Former members: Caroline Champenois, Rémi Delhuille, Alain Miffre
Visitors: Leszek Jozefowski (from Krakow) in 1998-1999
Our activity concerning atom interferometry began in 1994 by theoretical works on the refraction index of gases for atomic waves. Then, in 1996, we decided to set up an atom interferometer.
1. Introduction: our main choices
We choose to construct an atom interferometer, in which the interfering atomic beams are spatially separated. This separation is necessary to make interferometric measurements of a perturbation which must be applied on only one the two atomic beams inside the interferometer. We decided to work with thermal atoms mostly because the spatial separation achieved with cold atom interferometers are very small.
Our apparatus is a three-grating Mach-Zehnder interferometer. It shares several characteristics of the interferometers built by the research groups f D. Pritchard and of Siu Au Lee. Like D. Pritchard, we use an alkali atom seeded in a rare gas supersonic beam and, like Siu Au Lee, atom diffraction is performed by laser standing waves in the Bragg regime.
When using laser diffraction, the grating period is equal to half the laser wavelength. Because we must use a single frequency laser with a rather large power (hundreds of milliwatts) and a frequency tuned very close to an intense resonance transition of the atom, the choice of the laser wavelength results very directly from the choice of the atom and usually, because of all the requirements, the laser wavelength is in the visible range, so that the grating period is not very small. In order to get a not too small diffraction angle, we need a light atom and lithium was obviously the best choice, because of its small mass and of its intense first resonance transition at a 671 nm wavelength. At a velocity u = 1065 m/s, lithium atoms have a de Broglie wavelength equal to 54 pm. With a laser standing wave at a 671 nm wavelength, the grating period is 335 nm and the first order diffraction angle is close to 160 microradians.
Bragg diffraction by laser is an ideal tool to construct an atom interferometer as the atomic beam is divided in only two beams, one corresponding to the diffraction order 0 and the other the diffraction order p, which is selected by the incidence angle of the atomic beam on the laser standing wave. The diffraction efficiency can be adjusted between 0 and 100 % by varying the laser power density, the laser detuning from the atomic resonance or the interaction time of the atoms with the laser light.
We show in figure 1 a schematic drawing of our atom interferometer.
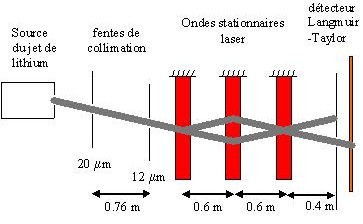
Figure 1: schematic drawing of our atom interferometer working with a thermal beam of lithium and laser diffraction in the Bragg regime.
2. Construction and optimisation of our atom interferometer
The construction of our interferometer really started in 1998 and, in July 2000, we first observed atom diffraction on a laser standing wave, in the Bragg regime. Then, we improved the operation of our hot-wire detector used for the detection of the atomic beam at the output of the interferometer and we developed the procedure necessary to align an atom interferometer. Alignment is quite complex as several angles must be tuned within typically 50 microradians to observe an interference signal and a few microradians to reach the optimum.
In 2001, we were able to observe very nice atom interference fringes, with a visibility V = (Imax - Imin)/ (Imax + Imin) equal to V = 74%, the best visibility obtained with an interferometer operating with thermal atoms. In our interferometer, the maximum separation between the two atomic beams is equal to 100 micrometers, close to the second laser standing wave ; this distance is close 2 000 000 times the atom de Broglie wavelength and, as shown by the high fringe visibility, the loss of coherence is quite small !
In July 2001, our experiment was stopped by a severe failure and many different problems were then encountered, thus forbidding a correct operation till the autumn of 2003. Since this date, we have been able to optimize in a systematic manner the tuning of our interferometer by a long series of experiments. Here are the main results:
![]() When using first order diffraction, we have observed a fringe visibility V = 84.5 1%
When using first order diffraction, we have observed a fringe visibility V = 84.5 1%
![]() We have observed interferences when using the 2nd and 3rd diffraction orders, with fringe visibilities which are still quite good, being equal to V = 54 % and V = 26 % respectively.
We have observed interferences when using the 2nd and 3rd diffraction orders, with fringe visibilities which are still quite good, being equal to V = 54 % and V = 26 % respectively.
![]() We have measured the dependence of the fringe visibility with the main alignment defects and our observations are very well explained by a theoretical calculation we had developed a few years ago.
We have measured the dependence of the fringe visibility with the main alignment defects and our observations are very well explained by a theoretical calculation we had developed a few years ago.
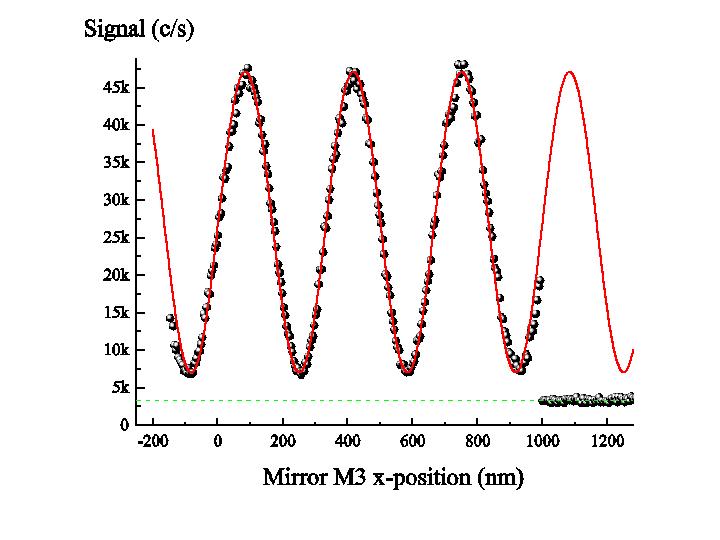
Figure 2: interference fringes recorded by sweeping the position of mirror M3 corresponding to the third laser standing wave. First order diffraction is used. The measured fringe visibility is V= 84.5 1%.
R. DELHUILLE, C. CHAMPENOIS, M. BÜCHNER, L. JOZEFOWSKI, Th. LAHAYE, R. MATHEVET, C. ROBILLIARD, A. MIFFRE, C. RIZZO, G. TRÉNEC and J. VIGUÉ, " Some theoretical and experimental aspects of three-grating Mach-Zehnder atom interferometers ", Comptes-Rendus de l’Académie des Sciences (Paris) IV, 2, 587-593 (2001)
R. DELHUILLE, C. CHAMPENOIS, M. BÜCHNER, L. JOZEFOWSKI, C. RIZZO, G. TRÉNEC and J. VIGUÉ, " High contrast Mach-Zehnder lithium atom interferometer in the Bragg regime ", Appl. Phys. B. 74, 489-493 (2002)
A. MIFFRE, M. JACQUEY, M. BÜCHNER, G. TRENEC and J. VIGUÉ, " Lithium atom interferometer using laser diffraction: description and experiments ", Eur. Phys. J. D 33, 99-112 (2005); preprint available on http://hal.ccsd.cnrs.fr/ccsd-00003124.
3. Experimental results and projects
a) Effect of a magnetic field gradient on the interference signals
b) Measurement of the electric static polarisability of Lithium atoms
c) Measurements of the refraction index of rare gases for atom waves
d) Related works: optimization of the hot wire detector
e) Related works: velocity distribution of the atomic beam
f) Related works : analysis of an three-grating Mach-Zehnder optical
interferometer
g) Construction of a powerful cw laser at 671 nm
h) Geometrical phase in quantum mechanics :
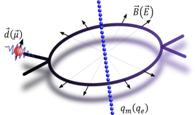
We measured the HMW phase shift predicted in 1993. This effect seems to be the last member of the geometric phase’s family detectable with free particles. This new example will stimulate further analysis leading to a deeper understanding of these phenomena.
4. Theoretical works
a) Index of refraction of gases for atom waves
b) Understanding how an atom interferometer works
c) Possible test the electric neutrality of atoms by atom interferometry
d) Phase noise on atom interference signals due to vibrations of the interferometer